Advanced Math Solutions – Ordinary Differential Equations Calculator

Differential equations contain derivatives, solving the equation involves integration (to get rid of the derivatives). We will cover the most common methods to solve ODE’s: linear, separable and Bernoulli.

• Linear first order equation is an ODE of the form y'(x)+p(x)y(x)=q(x)
• Separable equation is an ODE of the form N(y)dy=M(x)dx
• Bernoulli equation is an ODE of the form y'+p(x)y=q(x)y^n

You have first to identify the ODE type (can be tricky); then simply follow the steps as described below. 

Here’s an example of a separable equation (click here):

Simply solve by integrating both sides of the equation:

Here’s an example of a linear first order equation (click here):  

Steps to find the integration factor:

Here’s an example of a Bernoulli equation (click here):

In the next post we will take a closer look at each of the ODE types.

Cheers,

Michal

Advanced Math Solutions – Integral Calculator, integration by parts

Integration by parts is essentially the reverse of the product rule. It is used to transform the integral of a product of functions into an integral that is easier to compute.  Here’s the formula:
\int \:uv'=uv-\int \:u'v

In practice we have to choose u such that its derivative u’ is simpler, v’ such that its antiderivative v is simpler, and we want the multiplication of u’ and v easier to integrate than the multiplication of u and v’.

This is the last integration technique we cover for a reason.  But not to worry, there is a rule of thumb for choosing u, called ‘LIATE’ (simply choose u in that order), it stands for:

• Logarithmic functions
• Inverse trig functions
• Algebraic expressions
• Trig functions
• Exponential functions

Before we continue you might want to review common derivatives and common integrals.

Let’s start with some basic examples, this is one of the more intuitive examples.  If one of the multipliers is x, knowing the derivative of x is 1, simply choose u to be x (click here):

Here’s an example with logarithms (click here):

Here’s another example with algebraic expression and exponent (click here)

Here’s a tricky example choosing v’ to be 1 (click here):

In the next post we’ll cover some more advanced examples.

Cheers,
Michal

Advanced Math Solutions – Integral Calculator, inverse & hyperbolic trig functions

In the previous post we covered common integrals (click here).  There are a few more integrals worth mentioning before we continue with integration by parts; integrals involving inverse & hyperbolic trig functions. We kept these for later, as they are usually used with substitution.

• \int \frac{1}{x^2+1}dx=\arctan \left(x\right)+C
• \int \frac{1}{\sqrt{1-x^2}}dx=\arcsin \left(x\right)+C
• \int \frac{1}{1-x^2}dx=\arctanh \left(x\right)+C
• \int \frac{1}{\sqrt{1+x^2}}dx=\arcsinh \left(x\right)+C

Let’s take a look at a few examples, notice that we are trying to manipulate the functions to a known form (can be tricky)


Here’s an example using algebraic manipulation and substitution (click here):

Here’s another example using substitution to get to the common form (click here):

Here’s another example using substitution to get to the common form (click here):

Ready for integration by parts!


Cheers,
Michal

High School Math Solutions – Polynomial Long Division Calculator

Polynomial long division is very similar to numerical long division where you first divide the large part of the number, multiply the answer by the divisor, subtract and continue dividing the reminder until the reminder is smaller than the divisor.

With polynomials you do the same, only now you have to divide the higher order terms (first term of the numerator divide by the first term of the denominator).


Let’s start with a simple example  (click here):

Here’s another example this time with multiple iterations (click here):

Cheers,
Michal

High School Math Solutions – Partial Fractions Calculator

Partial fractions decomposition is the opposite of adding fractions, we are trying to break a rational expression into simpler fractions.  It takes a lot of work, but is extremely useful with integrals for instance (simplification can be a good strategy).  We start by factoring the denominator (if the numerator order is higher than the denominator we start with long division), then we write the partial fraction for each of the factors (watch out for high order factors), multiply and solve for the coefficients using the factors zeros.  Step by step examples can be really helpful here.

Let’s start with an example  (click here):

Here’s a more advanced example with high order factors (click here):

From here simply solve the equation and plug in the solutions to get the partial fractions.


Here’s an example where the order of the numerator is higher than the denominator (click here):

Cheers,
Michal

Advanced Math Solutions – Integral Calculator, trigonometric substitution

In the previous posts we covered substitution, but standard substitution is not always enough. Integrals involving radicals for instance, we want to get rid of the square root.
Here’s how:

• For \sqrt{a^2-bx^2}, let x=\frac{\sqrt{a}}{\sqrt{b}}\sin \left(u\right) and use the identity 1-\sin^2(u)=\cos^2(u)
• For \sqrt{a^2+bx^2}, let x=\frac{\sqrt{a}}{\sqrt{b}}\tan \left(u\right) and use the identity 1+\tan^2(u)=\sec^2(u)
• For \sqrt{bx^2-a^2}, let x=\frac{\sqrt{a}}{\sqrt{b}}\sec \left(u\right) and use the identity \sec^2(u)-1=\tan^2(u)

Here’s an example of tangent substitution (click here):

From here simply cancel, integrate and substitute back


Here’s an example of sine substitution (click here):

 
Here’s an example of secant substitution (click here):

We covered almost all there is to know about substitution.  In the next post we will cover inverse trigonometric functions.


Cheers,
Michal

Advanced Math Solutions – Integral Calculator, advanced trigonometric functions, Part II

In the previous post we covered integrals involving powers of sine and cosine, we now continue with integrals involving powers of secants and tangent of the form \tan^n(x)\sec^m(x).

The general rule to evaluate \int \tan^n\left(x\right)\sec^m\left(x\right)dx is as follows:

• If m is even and positive, take \sec^2(x) out, use the identity \sec^2(x)=1+\tan^2(x) to convert remaining sec to tan, and substitute u=\tan(x)
• If n is odd and positive, take \tan(x)\sec(x) out, use the identity \tan^2(x)=\sec^2(x)-1 to convert remaining tan to sec, and substitute u=\sec(x)
• If n is odd or even but there is no \sec(x) factor, use the identity \tan^2(x)=\sec^2(x)-1 and repeat the steps above
• If none of the cases apply, try converting to sine and cosine

Let’s see how it works starting with an example where m is even (click here):

Simply combine the solutions and substitute back u=\tan(x).

Here’s another example where n is odd (click here):

One more example where n is odd with no factor of sec(x) (click here):

In the next post we’ll cover trigonometric substitution, stay tuned.


Cheers,
Michal

Advanced Math Solutions – Integral Calculator, advanced trigonometric functions

In the previous post we covered substitution, but substitution is not always straightforward, for instance integrals involving powers of trig functions. We need first to transform the function into a more suitable form for substitution. We can do that using some manipulation and basic trig identities (we’ll show you all the tricks).

Here we will cover integrals of the form \sin^n(x)\cos^m(x).

The general rule to evaluate \int \sin^n(x)\cos^m(x)dx is as follows:

• If n is odd, take sin(x) out, use the identity \sin^2(x)=1-\cos^2(x), and substitute u=\cos(x)
• If m is odd, take cos(x) out, use the identity \cos^2(x)=1-\sin^2(x), and substitute u=\sin(x)
• If both n and m are odd use either n or m
• If both n and m are even use one of the half angle identities:
• \sin^2(x)=\frac{1-\cos(2x)}{2}
• \cos^2(x)=\frac{1+\cos(2x)}{2}
• \sin(x)\cos(x)=\frac{\sin(2x)}{2}

Let’s see how it works, starting with an example where m is odd (click here):

From here simply apply the sum rule and substitute back.


Here’s another example where n is odd (click here):

One more example where both n and m are even (click here):

In the next post we will continue with integrals involving powers of tan and sec.

Cheers,
Michal

Advanced Math Solutions – Integral Calculator, substitution

In the previous post we covered common integrals. You will find it extremely handy here b/c substitution is all about simplification, transforming the function into something more familiar.
At its basic form, substitution is used when an integral contains some function and its derivative. It is the reverse chain rule (click here for a quick review).

The substation rule is as follows:
\int f\left(g\left(x\right)\right)g^'\left(x\right)dx=\int f\left(u\right)du,\:\:\:where\:u=g\left(x\right)

Let’s see how it works, starting with the logarithmic function (click here):

Here’s an example of exponential functions (click here):

Here’s an example using the power rule (click here):

Here’s an example using simple trig substitution (click here):

Sometimes the appropriate substitution is not that obvious and requires some extra work.  We’ll walk you through more advanced examples in the next post

Cheers,
Michal

Advanced Math Solutions – Integral Calculator, common functions

In the previous post we covered the basic integration rules (click here).  Before we continue with more advanced techniques, we will cover some common integrals (reciprocal, exponential and trigonometric functions).  You will be using the common integrals a lot, so get to know them well.

Reciprocal & Exponential:
\int\frac{1}{x}dx=\ln|x|+C
\int e^x dx=e^x+C
\int a^x dx=\frac{a^x}{\ln(a)}+C

Trigonometry:
\int\cos(x)dx=\sin(x)+C
\int\sin(x)dx=-\cos(x)+C
\int\sec^2(x)dx=\tan(x)+C
\int\csc^2(x)dx=-\cot(x)+C

The remaining trig functions can be integrated using advanced techniques, but that’s for later.


Let’s take a look at a few examples (we’re doing it slowly)
Starting with basic trigonometric functions (click here):

Exponential function (click here):

Here’s an example using the sum rule, power rule, and common integrals (click here):

Still doing good.

Cheers,
Michal

Advanced Math Solutions – Integral Calculator, the basics

Integration is the inverse of differentiation.   Even though derivatives are fairly straight forward, integrals are not. Some integration problems require techniques such as substitution, integration by parts, trigonometric substitutions, or possibly more than one method.   We will walk you through slowly, starting with the basic integration rules:  the constant multiplication rule, the power rule, and the sum rule.

Some common functions you should get familiar with (we’ll show you more later):
\int a dx = ax + C
\int x dx = \frac{x^2}{2} + C

One more thing to remember, always add the constant of integration C.

Let’s start with the Power Rule: \int x^n dx = \frac{x^{n+1}}{n+1} + C,\quad n\ne-1
The power rule simply tells you to divide by n+1 (the power + 1) and increase the power by 1, it’s that simple.  Here’s an example of how it works (click here):

Let’s continue with the constant multiplication rule (click here):
\int af(x) dx = a\int f(x)dx

The constant multiplication rule simply tells to take out the constant

Moving on to the Sum Rule (click here):

Putting it all together (click here):

That wasn’t too bad.  If you’d like to take a pick at some more advanced integrals click here

Cheers,
Michal

Lies, Damned Lies, and Statistics

Statistics is about analyzing data, for instance the mean is commonly used to measure the “central tendency” of the data set (simply the average), or the median that measures the true middle of the data set.  Other basic methods that are fairly intuitive are the mode that finds the value that occurs most often, and the range that measures the difference between the largest and smallest numbers.  Some of the advanced methods that require more complex calculations are the variance, and standard deviation that measure how spread out the numbers are (measure of dispersion).

Why do we need all this?  To be able make decisions or even predictions based on a sample data set alone.  Symbolab now implements quite a few statistics methods to help you sort out the data step by step (No decisions, predications or “lies” just yet…).

Starting with the basics, here’s an example of the mean (click here)

here’s an example of the median (click here)

Let’s step up, here’s an example of the variance (click here)

Standard deviation, piece of cake (click here)

Click here to check the different statistics methods and examples

Cheers,
Michal

Back to School

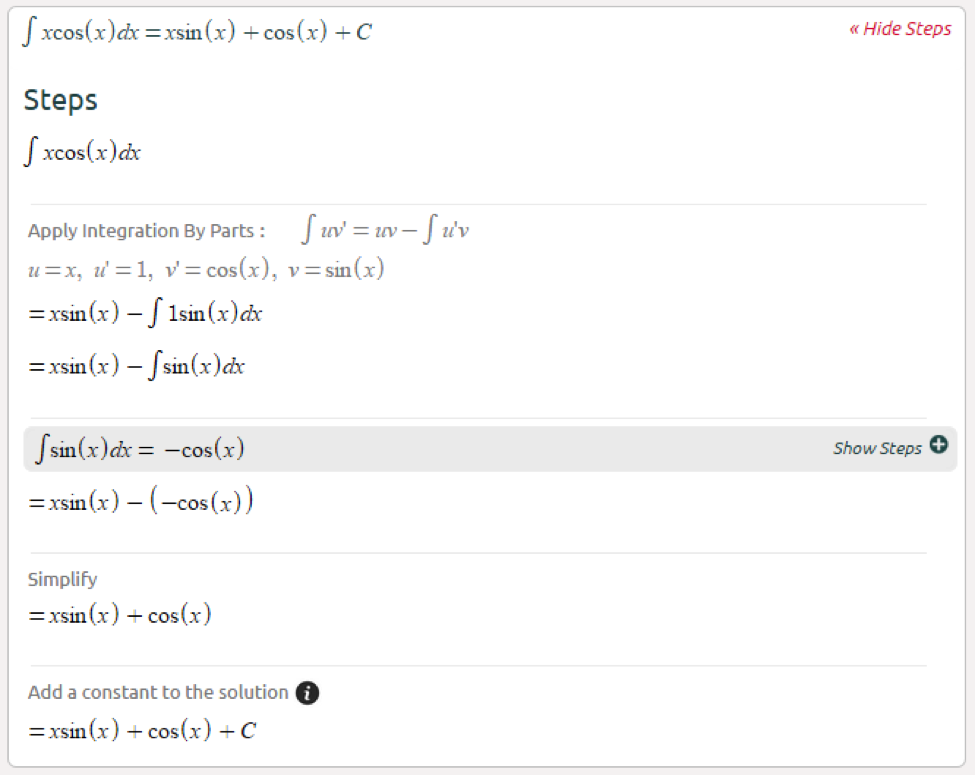
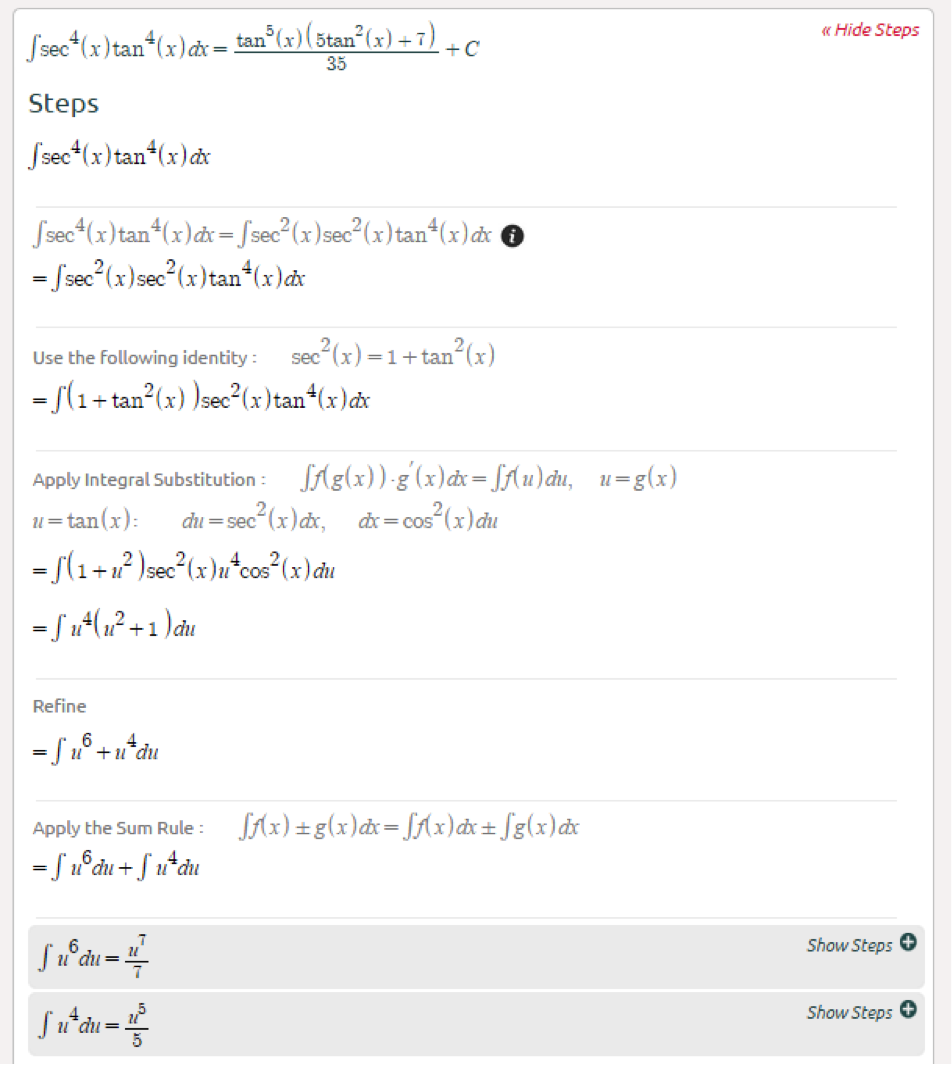
Are you ready for school?  We sure are.  We’ve added lots of new features to help you with math.

Factor:

Factoring polynomial expressions of any order. What for?  To find the zeroes of the polynomial for instance or to simplify complex expressions (we’ll show you examples of that too)

Here’s an example (click here):

For more factor examples click here.

Simplify:

Simplifying algebraic expressions and numbers (putting in the simplest form) using algebraic manipulations, factoring comes in handy.

Here’s an example (click here):

For more simplify examples click here.

Polynomials:

Solving polynomial equations of any order using factorization.

Here’s an example (click here):

For more polynomials examples click here.

Nonlinear System of Equations:

Nonlinear system of equations is a system in which at least one of the variables has an exponent other than 1 and/or there is a product of variables in one of the equations.  Solving nonlinear system of equations is somewhat trickier than solving linear system of equations.

Here’s an example (click here):

For more nonlinear system of equations examples click here.

Interactive Graphs:

You’ve already seen the interactive graphs for functions (click here for a quick review).  We’ve added clickable zoom and extra information on hover, and the interactive graphs are now available for equations and inequalities.  This is super cool!

Here’s an example (click here):

For more inequalities examples click here.

Take the time to play with the examples, send us comments, suggestions or questions on Facebook, Twitter, Feedback or email.  We want to hear from you.

You’re all set, have a great school year!

Cheers,
Michal

Functions

A function basically relates an input to an output, there’s an input, a relationship and an output.  For every input there is only one output.  This relationship between two variables is the most important in mathematics.

We want to understand the behavior of this relationship, in particular the domain, range, intercepts, parity, asymptotes, extreme points, and we want to draw the graph.

With Symbolab you can simply type in a function and with one click get all the properties with detailed steps, and an interactive graph that you can zoom in/our or move around.  You can also type in the property you’re looking for, for example domain or range (see functions menu for the full list of properties)

Let’s get started with a rational function (click here):

The graph showing the asymptotes and intercepts:

That’s a lot to digest.

Here’s another example of an exponential function (click here):

For more functions click here

Cheers,
Michal