In practice we have to choose u such that its derivative u’ is simpler, v’ such that its antiderivative v is simpler, and we want the multiplication of u’ and v easier to integrate than the multiplication of u and v’.
This is the last integration technique we cover for a reason. But not to worry, there is a rule of thumb for choosing u, called ‘LIATE’ (simply choose u in that order), it stands for:
- Logarithmic functions
- Inverse trig functions
- Algebraic expressions
- Trig functions
- Exponential functions
Before we continue you might want to review common derivatives and common integrals.
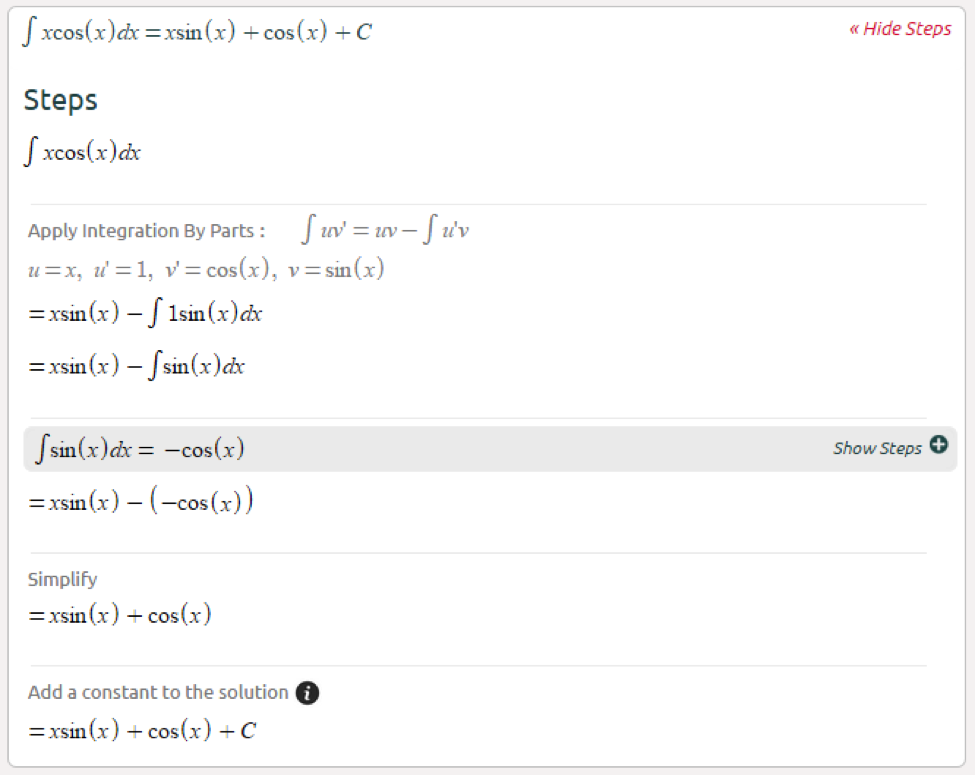
Let’s start with some basic examples, this is one of the more intuitive examples. If one of the multipliers is x, knowing the derivative of x is 1, simply choose u to be x (click here):
Here’s an example with logarithms (click here):
Here’s another example with algebraic expression and exponent (click here)
Here’s a tricky example choosing v’ to be 1 (click here):
In the next post we’ll cover some more advanced examples.
Cheers,
Michal