Advanced Math Solutions – Integral Calculator, advanced trigonometric functions, Part II

In the previous post we covered integrals involving powers of sine and cosine, we now continue with integrals involving powers of secants and tangent of the form \tan^n(x)\sec^m(x).

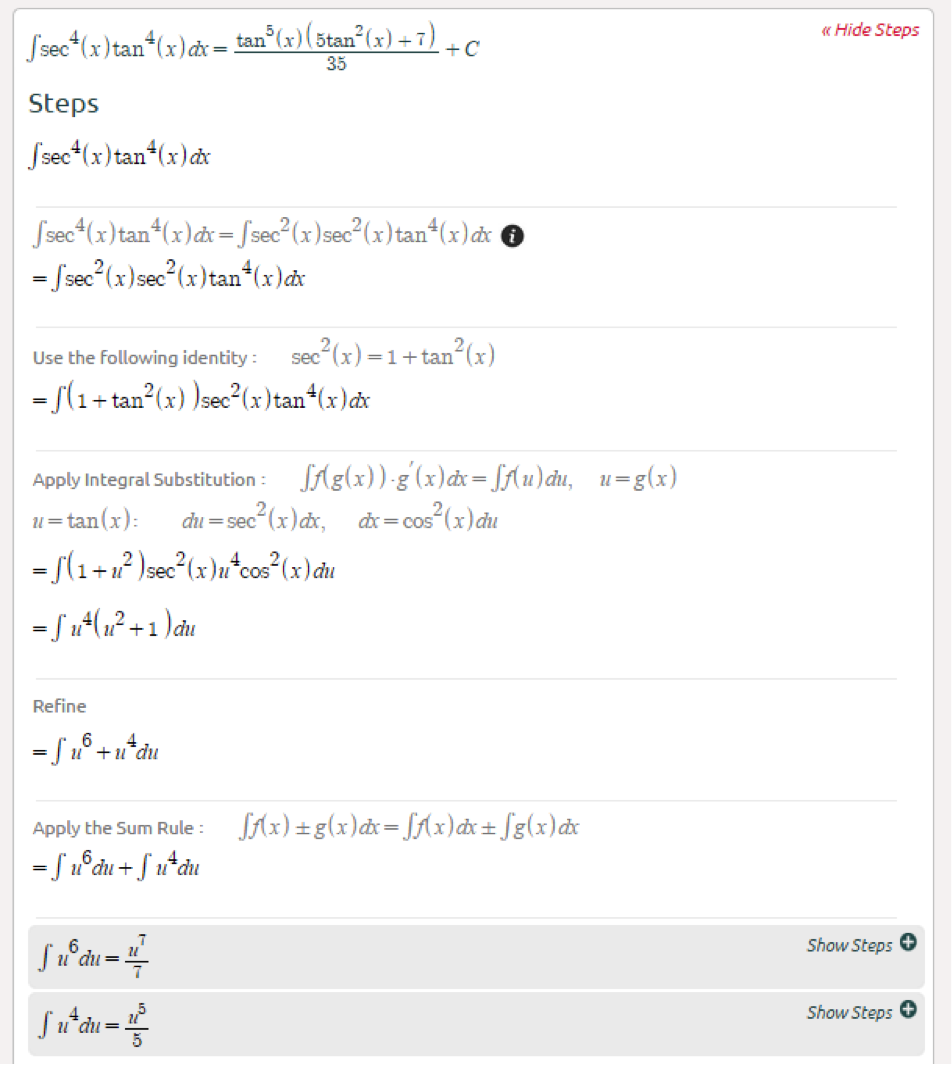
The general rule to evaluate \int \tan^n\left(x\right)\sec^m\left(x\right)dx is as follows:

• If m is even and positive, take \sec^2(x) out, use the identity \sec^2(x)=1+\tan^2(x) to convert remaining sec to tan, and substitute u=\tan(x)
• If n is odd and positive, take \tan(x)\sec(x) out, use the identity \tan^2(x)=\sec^2(x)-1 to convert remaining tan to sec, and substitute u=\sec(x)
• If n is odd or even but there is no \sec(x) factor, use the identity \tan^2(x)=\sec^2(x)-1 and repeat the steps above
• If none of the cases apply, try converting to sine and cosine

Let’s see how it works starting with an example where m is even (click here):

Simply combine the solutions and substitute back u=\tan(x).

Here’s another example where n is odd (click here):

One more example where n is odd with no factor of sec(x) (click here):

In the next post we’ll cover trigonometric substitution, stay tuned.


Cheers,
Michal

Advanced Math Solutions – Integral Calculator, advanced trigonometric functions

In the previous post we covered substitution, but substitution is not always straightforward, for instance integrals involving powers of trig functions. We need first to transform the function into a more suitable form for substitution. We can do that using some manipulation and basic trig identities (we’ll show you all the tricks).

Here we will cover integrals of the form \sin^n(x)\cos^m(x).

The general rule to evaluate \int \sin^n(x)\cos^m(x)dx is as follows:

• If n is odd, take sin(x) out, use the identity \sin^2(x)=1-\cos^2(x), and substitute u=\cos(x)
• If m is odd, take cos(x) out, use the identity \cos^2(x)=1-\sin^2(x), and substitute u=\sin(x)
• If both n and m are odd use either n or m
• If both n and m are even use one of the half angle identities:
• \sin^2(x)=\frac{1-\cos(2x)}{2}
• \cos^2(x)=\frac{1+\cos(2x)}{2}
• \sin(x)\cos(x)=\frac{\sin(2x)}{2}

Let’s see how it works, starting with an example where m is odd (click here):

From here simply apply the sum rule and substitute back.


Here’s another example where n is odd (click here):

One more example where both n and m are even (click here):

In the next post we will continue with integrals involving powers of tan and sec.

Cheers,
Michal

Advanced Math Solutions – Integral Calculator, substitution

In the previous post we covered common integrals. You will find it extremely handy here b/c substitution is all about simplification, transforming the function into something more familiar.
At its basic form, substitution is used when an integral contains some function and its derivative. It is the reverse chain rule (click here for a quick review).

The substation rule is as follows:
\int f\left(g\left(x\right)\right)g^'\left(x\right)dx=\int f\left(u\right)du,\:\:\:where\:u=g\left(x\right)

Let’s see how it works, starting with the logarithmic function (click here):

Here’s an example of exponential functions (click here):

Here’s an example using the power rule (click here):

Here’s an example using simple trig substitution (click here):

Sometimes the appropriate substitution is not that obvious and requires some extra work.  We’ll walk you through more advanced examples in the next post

Cheers,
Michal