Advanced Math Solutions – Ordinary Differential Equations Calculator

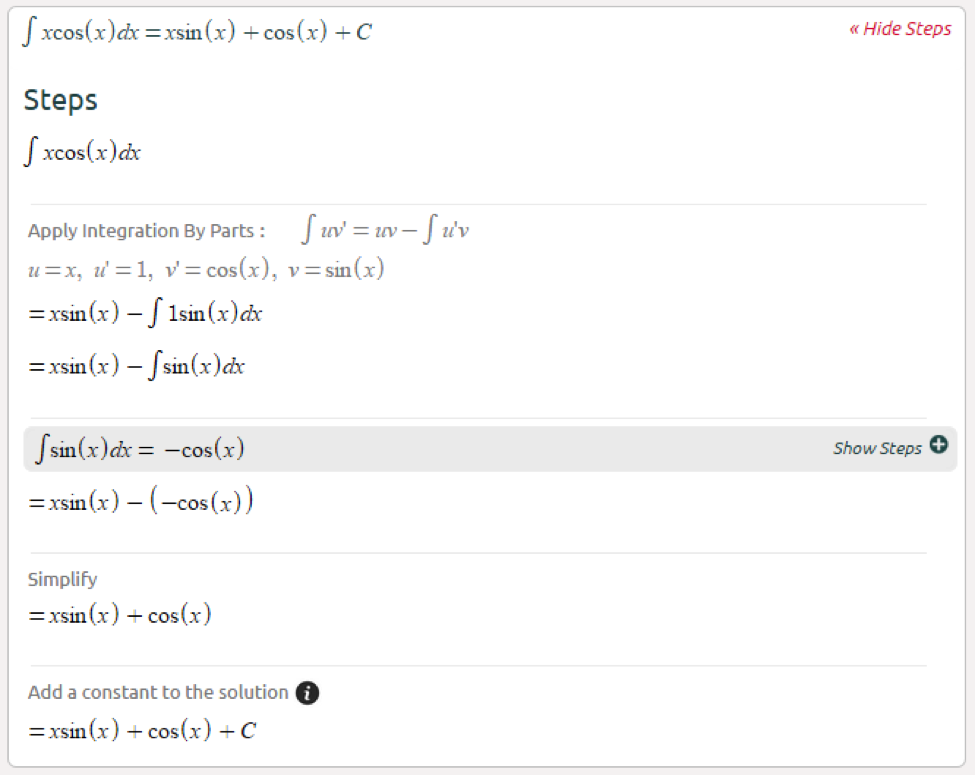
Differential equations contain derivatives, solving the equation involves integration (to get rid of the derivatives). We will cover the most common methods to solve ODE’s: linear, separable and Bernoulli.

• Linear first order equation is an ODE of the form y'(x)+p(x)y(x)=q(x)
• Separable equation is an ODE of the form N(y)dy=M(x)dx
• Bernoulli equation is an ODE of the form y'+p(x)y=q(x)y^n

You have first to identify the ODE type (can be tricky); then simply follow the steps as described below. 

Here’s an example of a separable equation (click here):

Simply solve by integrating both sides of the equation:

Here’s an example of a linear first order equation (click here):  

Steps to find the integration factor:

Here’s an example of a Bernoulli equation (click here):

In the next post we will take a closer look at each of the ODE types.

Cheers,

Michal

Advanced Math Solutions – Integral Calculator, integration by parts

Integration by parts is essentially the reverse of the product rule. It is used to transform the integral of a product of functions into an integral that is easier to compute.  Here’s the formula:
\int \:uv'=uv-\int \:u'v

In practice we have to choose u such that its derivative u’ is simpler, v’ such that its antiderivative v is simpler, and we want the multiplication of u’ and v easier to integrate than the multiplication of u and v’.

This is the last integration technique we cover for a reason.  But not to worry, there is a rule of thumb for choosing u, called ‘LIATE’ (simply choose u in that order), it stands for:

• Logarithmic functions
• Inverse trig functions
• Algebraic expressions
• Trig functions
• Exponential functions

Before we continue you might want to review common derivatives and common integrals.

Let’s start with some basic examples, this is one of the more intuitive examples.  If one of the multipliers is x, knowing the derivative of x is 1, simply choose u to be x (click here):

Here’s an example with logarithms (click here):

Here’s another example with algebraic expression and exponent (click here)

Here’s a tricky example choosing v’ to be 1 (click here):

In the next post we’ll cover some more advanced examples.

Cheers,
Michal

Advanced Math Solutions – Integral Calculator, inverse & hyperbolic trig functions

In the previous post we covered common integrals (click here).  There are a few more integrals worth mentioning before we continue with integration by parts; integrals involving inverse & hyperbolic trig functions. We kept these for later, as they are usually used with substitution.

• \int \frac{1}{x^2+1}dx=\arctan \left(x\right)+C
• \int \frac{1}{\sqrt{1-x^2}}dx=\arcsin \left(x\right)+C
• \int \frac{1}{1-x^2}dx=\arctanh \left(x\right)+C
• \int \frac{1}{\sqrt{1+x^2}}dx=\arcsinh \left(x\right)+C

Let’s take a look at a few examples, notice that we are trying to manipulate the functions to a known form (can be tricky)


Here’s an example using algebraic manipulation and substitution (click here):

Here’s another example using substitution to get to the common form (click here):

Here’s another example using substitution to get to the common form (click here):

Ready for integration by parts!


Cheers,
Michal