We’ve covered methods and rules to differentiate functions of the form y=f(x), where y is explicitly defined as a function of x (click here to review explicit differentiation). But what if we have to derive functions that are not set this way? If you can easily express y as a function of x, by all means do that first. For example x²+y=1, isolate y as a function of x: y= (1-x²) and use the derivative rules. Let’s look at x²+y²=1, or y=sin(3x+4y), clearly isolating y is not trivial, this is where we’ll be using implicit differentiation; Derive the left hand side and the right hand side with respect to x, and isolate y’. It is basically an application of the chain rule, just remember that y is not a constant, it is a function of x.
Let’s see how it works (click here):
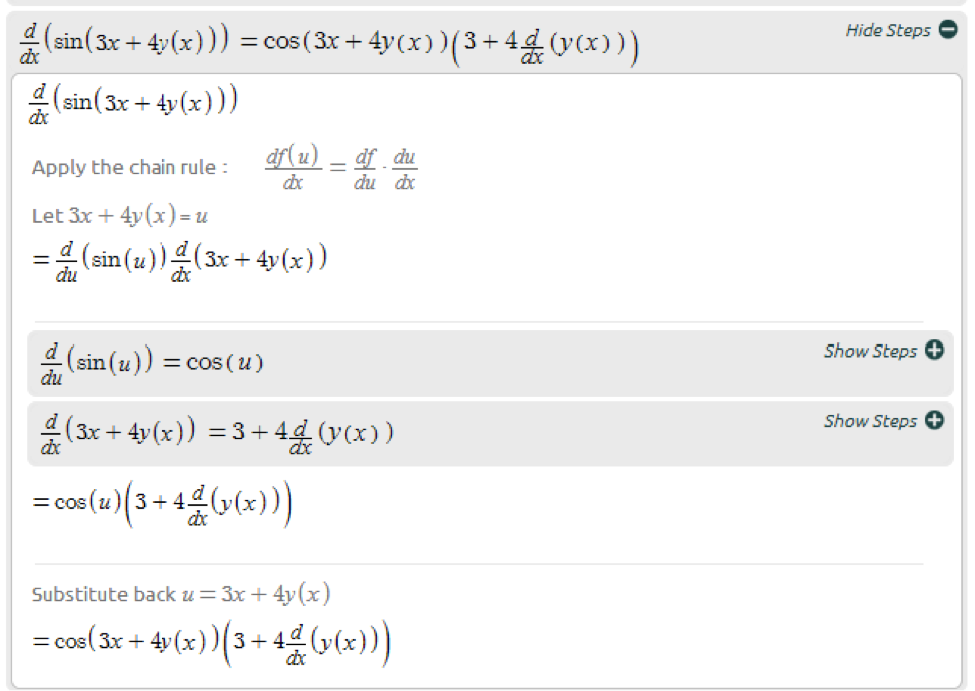
Now let’s take a closer look how to differentiate sin(3x+4y(x)) with respect to x:
Here’s another example, only this time differentiation with respect to y (click here):
Until next time,
Michal