The determinant is a value calculated from an matrix. The determinant of a matrix, A, can be denoted as det(A), det A, or |A|. There are many uses for determinants. The determinant can be used to solve a system of equations. The determinant can tell you if the matrix is invertible or not (it is not if the matrix is 0).
We will discuss three ways to solve three different types of matrices.
Determinant of a 2x2 matrix:
1. Put the matrix in REF (here is the blog post on REF for reference)
2. Calculate the product of the elements in the diagonal
- Make note of how many times you swapped rows to achieve putting the matrix in REF
- If no rows were swapped, this is the determinant
3. If rows were swapped, multiply the product of the elements in the diagonal by (-1) raised to the number of times rows were swapped. This will give you the determinant.
- Swapping rows changes the sign of the determinant
Let’s see some examples to better understand how to calculate the determinant.
First example (click here):
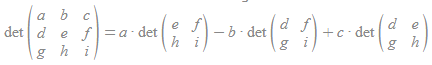
Note that rows were swapped 3 times to achieve putting the matrix in REF.
2. Calculate the product of the diagonal
Until next time,
Leah

















