Advanced Math Solutions – Derivative Calculator, Implicit Differentiation

We’ve covered methods and rules to differentiate functions of the form y=f(x), where y is explicitly defined as a function of x (click here to review explicit differentiation).  But what if we have to derive functions that are not set this way?  If you can easily express y as a function of x, by all means do that first.  For example x²+y=1, isolate y as a function of x:  y= (1-x²) and use the derivative rules.  Let’s look at x²+y²=1,  or y=sin(3x+4y), clearly isolating y is not trivial, this is where we’ll be using implicit differentiation;  Derive the left hand side and the right hand side with respect to x, and isolate y’.  It is basically an application of the chain rule, just remember that y is not a constant, it is a function of x.


Let’s see how it works (click here):

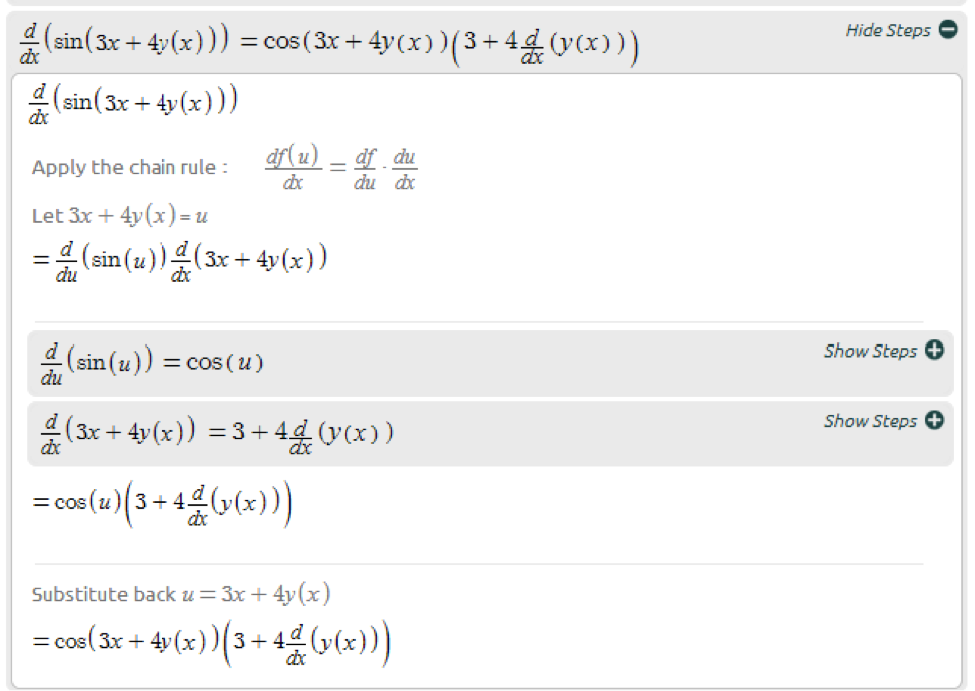
Now let’s take a closer look how to differentiate sin(3x+4y(x)) with respect to x:

Here’s another example, only this time differentiation with respect to y (click here):

Until next time,
Michal

High School Math Solutions – Absolute Value Inequalities Calculator

In the last post we covered absolute value equations (click here for the previous post) and the need for understanding the absolute value property. Here, solid understanding of the inequality property is required as well, which makes absolute value inequalities more challenging (click here for a quick review of inequalities).

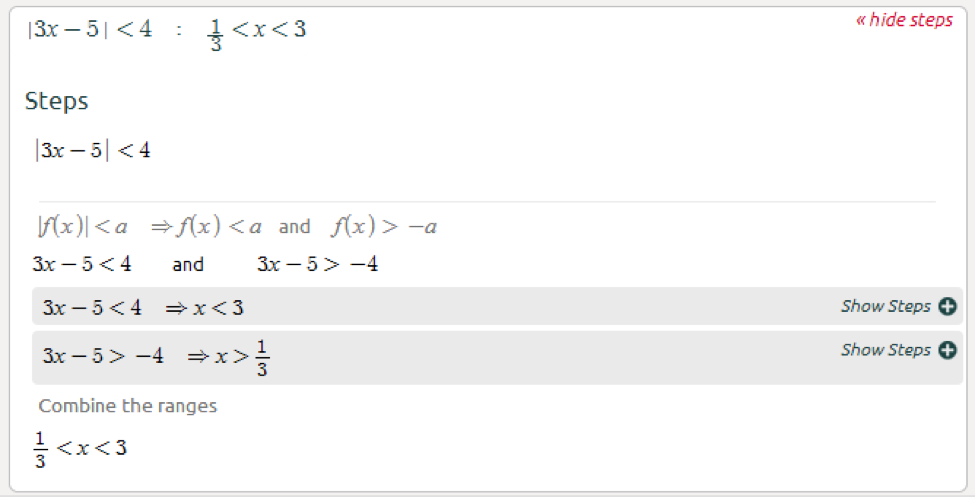
Let’s start with simple absolute value inequalities:

• For inequalities of the form |f(x)| < a the solution is always –a < f(x) < a
• For inequalities of the form |f(x)| > a the solution is always f(x) < -a or f(x) > a

Either way, this leaves us with two simple inequalities to solve.

Here's how it works (click here):

Here's another example (click here):

Solving inequalities involving variables is very similar to solving absolute value equations with variables. You should first find the positive and negative ranges of the absolute values.  Write the simple inequalities for the different ranges, solve and validate the solutions are within the range.

Here's how it works (click here):

If you’re up for a challenge try this one    

Or click here for the solution…


Until next time,
Michal