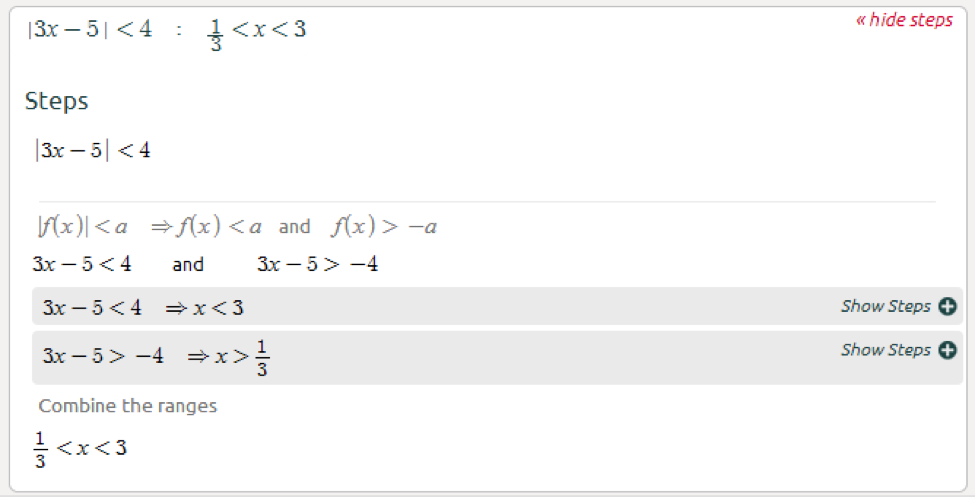
Let’s start with simple absolute value inequalities:
- For inequalities of the form |f(x)| < a the solution is always –a < f(x) < a
- For inequalities of the form |f(x)| > a the solution is always f(x) < -a or f(x) > a
Either way, this leaves us with two simple inequalities to solve.
Here's how it works (click here):
Here's another example (click here):
Solving inequalities involving variables is very similar to solving absolute value equations with variables. You should first find the positive and negative ranges of the absolute values. Write the simple inequalities for the different ranges, solve and validate the solutions are within the range.
Here's how it works (click here):
If you’re up for a challenge try this one
Or click here for the solution…
Until next time,
Michal