Product rule: (fg)’ = f’g + g’f
Quotient rule: (f/g)'=(f'g+g'f)/g^2
Let’s start with an example using the product rule, (click here):
Here’s an example using the quotient rule (click here):
Until next time,
Michal
Tuesday, January 7, 2014
High School Math Solutions – Derivative Calculator, Products & Quotients
In the previous post we covered the basic derivative rules (click here to see previous post). We are now going to step up a bit to differentiate products & quotients. Functions involving products and quotients seem more complex, but once you follow the derivative rules it’s straightforward. Start by identifying the different components (i.e. multipliers and divisors), derive each component separately, carefully set the rule formula, and simplify.
Product rule: (fg)’ = f’g + g’f
Quotient rule: (f/g)'=(f'g+g'f)/g^2
Let’s start with an example using the product rule, (click here):
Here’s an example using the quotient rule (click here):
Until next time,
Michal
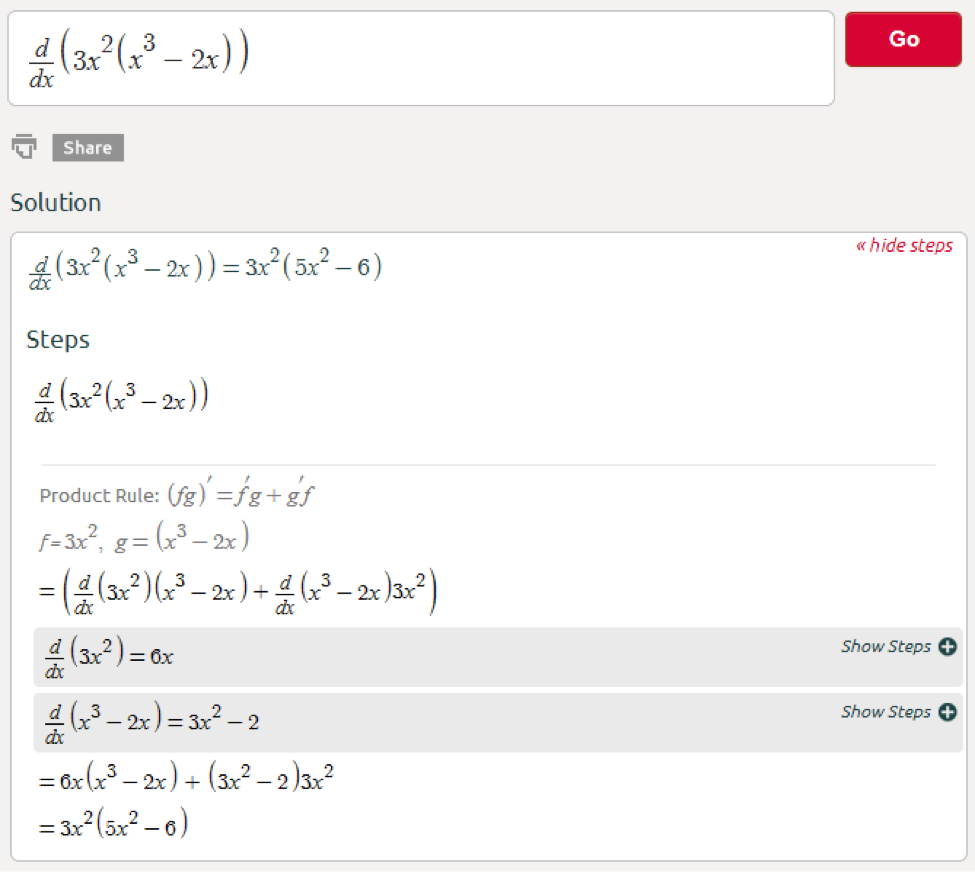
Product rule: (fg)’ = f’g + g’f
Quotient rule: (f/g)'=(f'g+g'f)/g^2
Let’s start with an example using the product rule, (click here):
Here’s an example using the quotient rule (click here):
Until next time,
Michal
