Advanced Math Solutions - Matrix Inverse Calculator, Determinants

Last blog post, I talked about what the inverse of a matrix is. In this blog post, I will go over what the determinant of matrix is and how to calculate.

The determinant is a value calculated from an n\times n matrix. The determinant of a matrix, A, can be denoted as det(A), det A, or |A|. There are many uses for determinants. The determinant can be used to solve a system of equations. The determinant can tell you if the matrix is invertible or not (it is not if the matrix is 0).

We will discuss three ways to solve three different types of matrices.

Determinant of a 2x2 matrix:

Determinant of a 3x3 matrix:

Determinant of a nxn matrix that is 4x4 or larger:

1. Put the matrix in REF (here is the blog post on REF for reference)

• Make note of how many times you swapped rows to achieve putting the matrix in REF 

2. Calculate the product of the elements in the diagonal

• If no rows were swapped, this is the determinant

3. If rows were swapped, multiply the product of the elements in the diagonal by (-1) raised to the number of times rows were swapped. This will give you the determinant.

• Swapping rows changes the sign of the determinant

Let’s see some examples to better understand how to calculate the determinant.

First example (click here):

1. Use this formula:

Next example (click here):

1. Use this formula: 

Last example (click here):

1. Put the matrix in REF

Since there is already a blog post on how to put a matrix in REF, I am not going to go through the steps for doing this. You can look at the link for this last example to see how to do this.

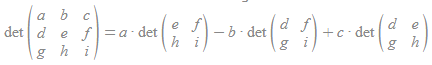
Note that rows were swapped 3 times to achieve putting the matrix in REF.

2. Calculate the product of the diagonal

3. If rows were swapped, multiply the product of the diagonal by (-1) raised to the number of times rows were swapped.

As you can see, this is a lot of material to learn and remember. Don’t let it intimidate you! Once you start practicing, it will get easier. For more help or practice on this topic, check out Symbolab’s Practice. Next blog post, I will talk about a shortcut for calculating the inverse of a 2x2 matrix, using its determinant.
Until next time,

Leah